概率与似然
一对好伙伴

世界杯已经进行了半个多月了,早已经有黑眼圈了。
这届世界杯真是冷门频发,转折不断,可谓精彩纷呈,有人欢喜有人忧。有人中大彩,有人上天台。

(你个几百块钱的就不要挤上来了)

世界杯球赛的结果是如此错综复杂,以致于很少有人能够准确地预测出每一场球赛的结果。
在这种变幻莫测的运动赛事中,当然离不开概率。今天,超模君就从世界杯球赛的角度来简单介绍下概率以及他的好基友——似然。

那么先来说大家是如何判断一场比赛的结果呢?
一般大家会通过各种信息,如比赛队伍双方世预赛或者其他赛事的输赢情况、进球数等等判断双方的综合实力,将这些已有的信息称之为参数。根据这些参数,就可以对比赛结果进行推测,得到比赛各种结果的可能性,这就是概率。

举个相对简单的例子,一场球赛开赛前,裁判会通过掷硬币的方式决定双方的场地选择权。

把硬币的正面朝上出现的概率称为硬币的参数。假设硬币是完全公平的,则硬币正面与反面出现的概率是相同的,都是0.5,即硬币的参数是0.5。
于是可以推测,投掷10次硬币,出现5次正面朝上的概率是:
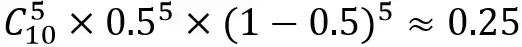
这种根据已有信息即参数推测结果的各种可能性的方式就是求概率。
那么似然又是什么呢?

“似然”这个词是对英文likelihood的一种较为贴近文言文的翻译,用现代的中文来说就是“可能性”。
概率是在已知一些参数的情况下,预测接下来的观测所得到的结果。
而似然则是用于在已知某些观测所得到的结果时,对有关事物的性质即参数进行估计。
比如说,在掷硬币之前,我们并不知道硬币是否是公平的,对硬币自身的性质即参数一无所知,但我们可以根据掷硬币的结果推测出硬币的大致参数,这就称作似然。
再粗略举一个比赛中的例子,小组赛F组德国对阵墨西哥。根据德国是上届世界杯的冠军,而墨西哥止步于十六强,可以推测德国队综合实力比墨西哥队强的概率为“高”,即参数为“高”。

进一步收集更多的信息,发现德国在预选赛取得全胜的优异战绩,墨西哥则是5胜2平1负。所以,进一步推出参数为“很高”。
再看看先前两队的交战情况。历史上,两队在世界杯交手3次,德国保持不败。1978年世界杯小组赛德国6-0大胜墨西哥。1986年世界杯1/4决赛,两队120分钟战成0-0,点球战德国4-1胜出;1998年世界杯1/8决赛,德国2-1逆转墨西哥。于是,可以认为参数最大的可能性为“极高”,也就是说,德国队最有可能比墨西哥要强很多。

这种通过已有结果信息,对原参数进行推断,称作似然。而推测出最可能的参数值,称为极大似然估计。
我们会有这样的感觉,当已有的结果信息越多时,即实验结果越多,得到的参数可能就越明确。
再举个例子,出乎人的意料,强大的德国队败给了墨西哥队。如果只根据这一结果对参数进行推测,就推出了参数最有可能为“低”,即德国队综合实力最有可能没有墨西哥队强。
这种说法显然有些片面,但这就是似然的本质逻辑。


实际上,当实验结果越来越多时,推测出的参数值就会更精准。
我们对掷硬币的例子进行具体分析,掷10次硬币,发现有6次正面朝上。
我们对该硬币的性质一无所知,所要推测的就是其最可能的参数值。假设这枚硬币是完全公平的,即硬币的参数是0.5,由此计算出以上实验结果出现的概率为:
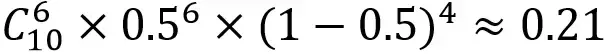
当然,硬币也有可能是不公平。设硬币的参数为0.6,则实验结果出现的概率是:
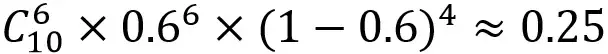
可以看出,参数为0.6使得实验结果出现的概率要比参数为0.5时的大,即以0.6作为参数的可能性更大,该硬币更倾向于是不公平的。
为了进一步推出最可能的参数值,进行极大似然估计。设硬币的参数为
,则似然函数为:
作出似然函数的图像:
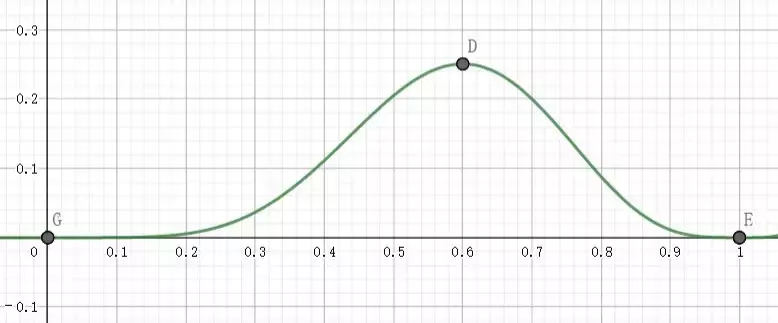
从图像中可以看出,参数值为0.6时,概率最大。D(0.6,0.25)为极值点。当参数值大于或小于0.6时,概率逐渐递减。0.6为最可能的参数值。
所以要进行极大似然估计,就是要找到似然函数的极值。
增加实验次数,设已知50次投掷结果,求出现30次正面朝上时硬币的参数,似然函数的图像如下:
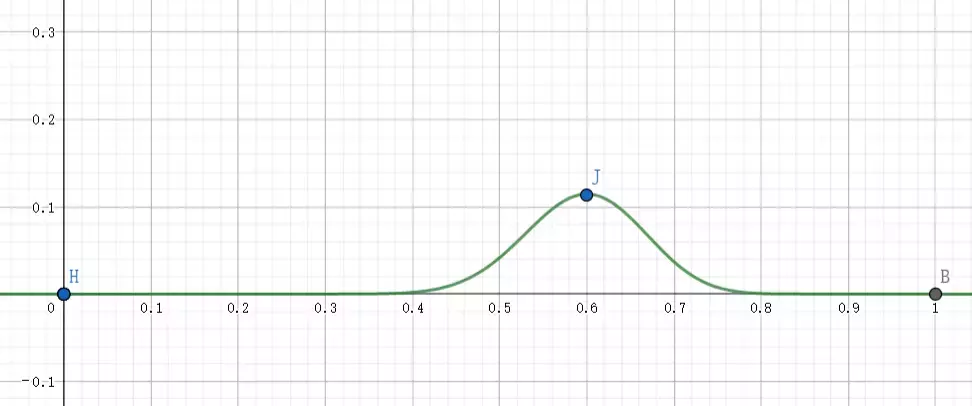

从图中明显可以看出,似然函数大于0的范围收缩了,也就是说,可以选择的参数值的分布更加集中了。
随着已知实验结果的增多,我们对事物的性质越来越了解,参数也会越来越明确。
极大似然估计法教会了我们世界压强队更容易赢,但却没告诉我们这届世界杯爱爆出冷门,你看,德国、阿根廷、葡萄牙、西班牙都回家了,其他所谓的强队还会远吗?
本文由超级数学建模编辑和整理
部分资料来源于网络
转载请在公众号中,回复“转载”
-----这里是数学思维的聚集地------
“超级数学建模”(微信号supermodeling),每天学一点小知识,轻松了解各种思维,做个好玩的理性派。60万数学精英都在关注!
「征稿启事」
超模现正式向粉丝们公开征稿!内容须原创首发,与数学、物理相关,一经采用,会奉上丰厚稿酬,详情请戳。

 十大足球直播推荐
十大足球直播推荐











